Один многорукий бандит против всех А/Б-тестов

2020-03-10

(Image source: UC Berkeley AI course slide, lecture 11.)

Когда хочется добавить в продукт новую фичу, поменять имеющуюся или изменить формулу построения рекомендации, обычно вспоминают про классические А/Б-тесты.

Как они проводятся? Пользователей делят на две группы, придумывают метрику, показывают каждой группе свою версию фичи. Через некоторое время по метрике оценивают, какая версия лучше. Более подробно останавливаться на А/Б-тестах я не буду.

Подход стандартный, более-менее понятный, подробно описан, но не лишен проблем:

требуется ручная поддержка процесса: нужно запускать исследования, рассчитывать пороги принятия решения. Нужен человек, который будет следить за процессом.
предполагается, что поведение пользователей не меняется со временем.
часть пользователей будет видеть неудачные варианты фичи больше времени, чем могли бы.

Существует другой, менее известный подход, согласно которому можно просто зарелизить фичу, а выбор варианта фичи для показа предоставить алгоритму. Более того, можно даже учитывать изменения предпочтений пользователей со временем.

О чём же речь? Знакомьтесь:

Многорукие бандиты

Идея довольно простая. Представим игральный автомат типа "однорукий бандит": кидаешь монетку, дёргаешь ручку и иногда (с заданной вероятностью, распределением, вероятностным правилом или законом) получаешь выигрыш, большой или не очень, — всё зависит от того, насколько жаден владелец автомата.

"Многорукий бандит" — это математический аналог, придуманный по образу и подобию реального однорукого прототипа и отличается от него немногим — у него просто несколько рук (или — ручек).
Каждая ручка обладает своими свойствами (вероятностным законом), и какая-то ручка работает лучше, и если бы ты знал с самого начала про эту ручку, то в среднем выигрывал бы чаще и больше.
Ручки на вид все одинаковые и заранее (пока не дёрнешь за них) неизвестно, какая ручка как себя ведёт.

Если переформулировать в терминах веб-разработки: когда выпускаешь новый вариант фичи или меняешь формулу ранжирования результатов, ты так же не знаешь, насколько новая фича будет полезна пользователю, и какой вариант фичи, формулы ему показать.

Для чего многорукий бандит в продакшене

Тут всё просто: релизишь новый вариант фичи — у многорукого бандита появляется новая ручка. Каждый раз, когда пользователь обращается за фичей, алгоритм многорукого бандита принимает решение, какой вариант фичи показывать пользователю (или формулу, или какой алгоритм рекомендации применять).

Когда алгоритм многорукого бандита понимает, что тот или иной вариант фичи чаще даёт лучший результат, он начинает показывать его всё чаще. Плохие варианты фичи показываются пользователю всё реже.

В зависимости от постановки задачи может так случиться, что вариант фичи вдруг или со временем начинает нравиться пользователям больше, чем раньше. В таком случае алгоритм должен будет плавно переключиться на использование этого варианта фичи.

Итак, в отличие от А/Б-тестов, применение многоруких бандитов позволяет:

автоматически вводить фичу в строй при успехе фичи у пользователей,
автоматически реагировать на изменения предпочтений пользователей,
автоматически переключиться со "сломанного" варианта фичи при падении части инфраструктуры.
без подготовки проводить как эксперимент, так и процедуру оценки результата.

Алгоритм многорукого бандита балансирует между двумя задачами:

Эксплуатация (exploitation) — извлечение прибыли из текущих знаний о ручках.
Исследование (exploration) — добыча новых знаний: может быть, есть такая ручка, которая приносит больше выигрыша? Какая-то ручка вдруг заработала лучше?

Такая дилемма типична для задач из раздела машинного обучения — Обучение с подкреплением (Reinforcement learning).

Среда обитания многорукого бандита

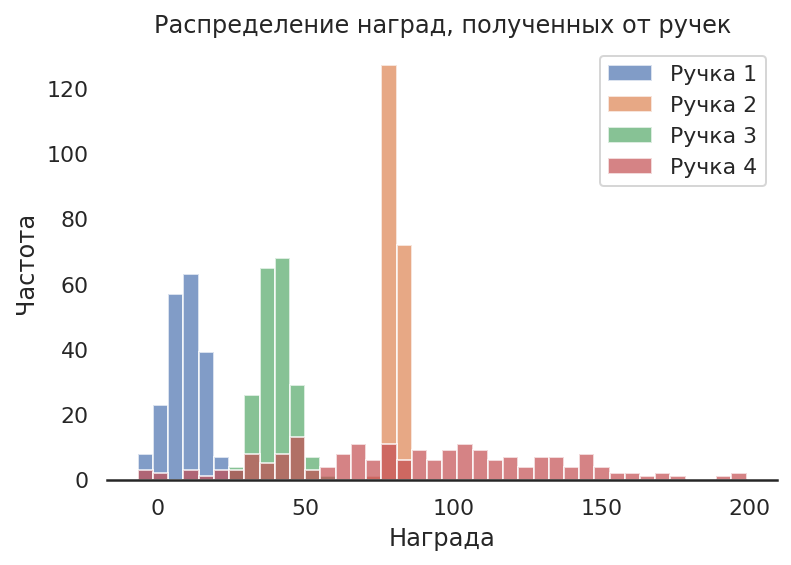
Для того чтобы посмотреть, как работает многорукий бандит, нам нужна модель его "рук". Например, если мы используем многорукое чудище для того, чтобы показывать разные версии сайта. А за "награду" возьмем конверсию — процент посетителей, который остался на нашем сайте после показа конкретной версии сайта.

Мы заранее не знаем, какие факторы могут повлиять на то, что пользователь останется или уйдёт от нас. Но мы можем с некоторой долей уверенности предположить, что таких факторов много.

В такой постановке мы можем воспользоваться Центральной предельной теоремой, а именно — тем фактом, что сумма множества случайных факторов (величин) приводит к появлению нормального распределения.

Тогда мы можем смоделировать выигрыш от использования "руки" многорукого бандита измерением (выборкой) нормально распределённой случайной величины с заданными параметрами дисперсии и матожидания. При этом разными для каждой из рук.

Но на самом деле это всё допущение, никаких гарантий, что распределение в конкретной задаче будет нормальным, нет. Но это не запрещает использовать многоруких бандитов в задаче.

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
%config InlineBackend.figure_format='retina'
sns.set(style="white", rc={
                           'axes.spines.left': False,
                           'axes.spines.right': False,  
                           'axes.spines.top': False })
rs = np.random.RandomState(2322)

def arm_A():
    return rs.normal(10, 6)
def arm_B():
    return rs.normal(20, 10)
def arm_C():
    return rs.normal(40, 6)
def arm_D():
    return rs.normal(90, 10)

df = pd.DataFrame({
    "Ручка 1" : [arm_A() for x in range(200)],
    "Ручка 2" : [arm_B() for x in range(200)],
    "Ручка 3" : [arm_C() for x in range(200)],
    "Ручка 4" : [arm_D() for x in range(200)]})

ax = df.plot.hist(bins=40, alpha=0.7)
ax.set_title("Распределение наград, полученных от ручек")
plt.ylabel('Частота')
plt.xlabel('Награда');

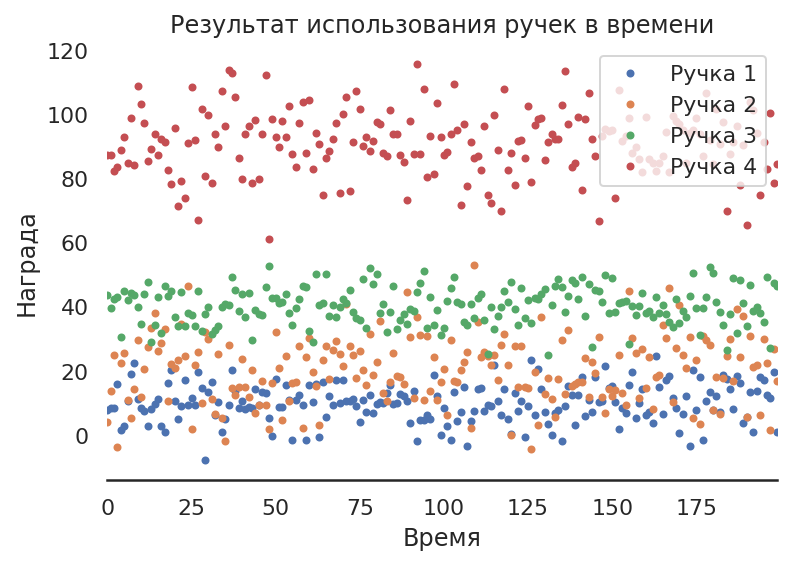
ax = df.plot.line(style='.')
ax.set_title("Результат использования ручек в времени");
plt.xlabel('Время')
plt.ylabel('Награда');

Какие модели бандитов бывают?

В зависимости от решаемой задачи существует выбор модели бандита. Среди самых популярных:

Multi-armed bandit — каждая ручка задаётся плотностью вероятности награды.
Binary multi-armed bandit (Benulli multi-armed bandit) — награда у всех ручек фиксированная и одинаковая. Но выдаётся награда, только с вероятность p, различной для каждой ручки. C вероятностью 1 - p награда не выдаётся.
Restless multi-armed bandit — каждая ручка может со временем менять своё поведение (плотностью распределения вероятности).
Sleepy multi-armed bandit — ручки могут пропадать и возникать снова, становиться и переставать быть доступными в конкретных раундах.
Mortal multi-armed bandit — ручки исчезают и больше не возвращаются.
Contextual Multi-Armed Bandits — награда ручки зависит от того кто, ей пользуется, например, от конкретного пользователя.

Простые алгоритмы

Greedy ("Жадный") — алгоритм выбирает самую первую ручку, которая даёт любой положительный результат, и использует её. Каких-то дополнительных исследований алгоритм не производит.
100% Исследователь — алгоритм просто выбирает случайную ручку из всех доступных.

Всё просто и не работает, и не решает задачу. Но это просто крайности. Идём дальше.

ε-greedy (эпсилон "жадный")

Бандит как бы подбрасывает необычную монетку каждый раз, когда нужно принять решение. Монетка отличается от обычной тем, что падает на одну сторону с вероятностью ε, а на другую — с вероятностью 1 - ε.

В зависимости от того, в какую сторону упала монетка, мы принимаем решение, дергаем ту ручку, про которую мы знаем, что она приносит в среднем больше выигрыша, чем все остальные, либо дергаем любую другую ручку и записываем, сколько выигрыша она принесла.

Лучшая ручка выбирается довольно просто, через обыкновенное среднее:

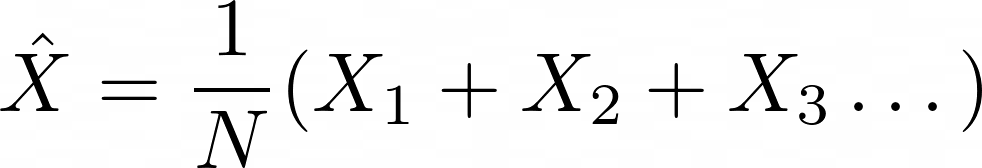
где N — число экспериментов, X1,X2 ... Xn — награды за 1-е, 2-е...энное использование ручки.

Заметим, что Жадный и 100% Исследователь получаются, когда ε выставляется в 0.0 и в 1.0.

Откуда взялось название ε-greedy?

"Жадными" в информатике называются алгоритмы, принимающие решение без оглядки на будущее, исходя из текущей ситуации. ε-greedy в данном контексте означает, что с вероятностью ε будет принято "жадное" решение дёрнуть самую лучшую на данный момент ручку, даже если на самом деле лучшая ручка другая, просто другие ручки мы недостаточно исследовали.

Реализация

def do_nth_arm(n):
    arms = {
        0 : arm_A, 
        1 : arm_B,
        2 : arm_C,
        3 : arm_D}
    return arms[n] ();

def egreed_get_best_arm(stats):
    top = 0;
    top_arm = 0
    for arm,arm_rewards in stats.items():
        avg_reward =  (1.0/len(arm_rewards)) * sum(arm_rewards)
        if top < avg_reward:
            top_arm = arm
            top = avg_reward
    return top_arm

def mab_egreed(p,armstats,runs):
    rn = rs.rand();
    arm = 0
    reward = 0
    if rn > p:
        arm = egreed_get_best_arm(armstats)
        reward = do_nth_arm(arm)
    else:
        arm = rs.choice(4)
        reward = do_nth_arm(arm);
    
    armstats[arm].append(reward)
    runs[arm] =  runs.get(arm, 0) + 1
    
    return armstats,runs

def mab_egreedrun(eps):
    armstats = {x: [y] for x, y in zip(range(4), [0]*4)}  
    runs = {}
    mA,mB,mC,mD = [],[],[],[]
    r = [mA,mB,mC,mD]
    for g in range(80):
        n = 10
        for _ in range(0,n):
            _, runs = mab_egreed(eps,armstats,runs)
    
        [r[x].append(runs.get(x,0)) for x in range(4)]
    return r

def plot_runs(title,mA,mB,mC,mD):
    data = pd.DataFrame({'model_A':mA,
                     'model_B':mB,
                     'model_C':mC,
                     'model_D':mD }, index=range(len(mA)))
 
    data_perc = data.divide(data.sum(axis=1), axis=0)
     
    labels = ["Ручка 1","Ручка 2","Ручка 1","Ручка 4"] 
    
    plt.figure(figsize=(16, 5))
    plt.stackplot(range(len(mA)),  
              data_perc["model_A"],  
              data_perc["model_B"],  
              data_perc["model_C"], 
              data_perc["model_D"],
                  labels=labels)
    plt.legend(loc='upper left')
    plt.box(False)
    plt.yticks([])
    plt.title(title)
    plt.xlabel('Время')
    plt.ylabel('Доли использования ручки');

Попробуем выставить ε = 1.0 (бандит в 100% случаев будет заниматься исследованием).

runs = mab_egreedrun(1.0);
plot_runs("Прогон с ε = 1.0",*runs)

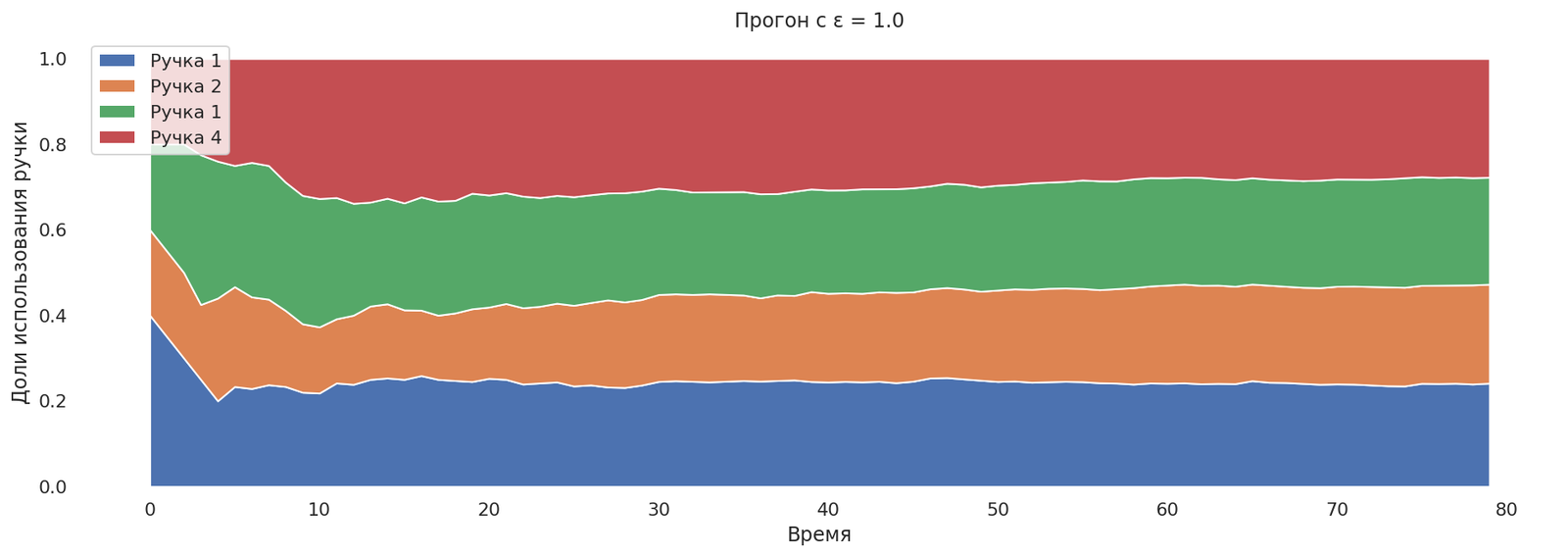
Все ручки исследуются в равной пропорции.

Примерно так же может выглядеть проведение А/Б-теста в четырёх вариантах с равным разделением аудитории. Что показывает неэффективность А/Б-тестирования. Многорукий бандит может найти лучшии вариант фичи гораздо быстрее, чем человек примет решение, что будет показано далее.

Попробуем выставить ε = 0.0 — теперь сделаем бандита на 100% жадным.

runs = mab_egreedrun(0.0);
plot_runs("Прогон с ε = 0.0",*runs)

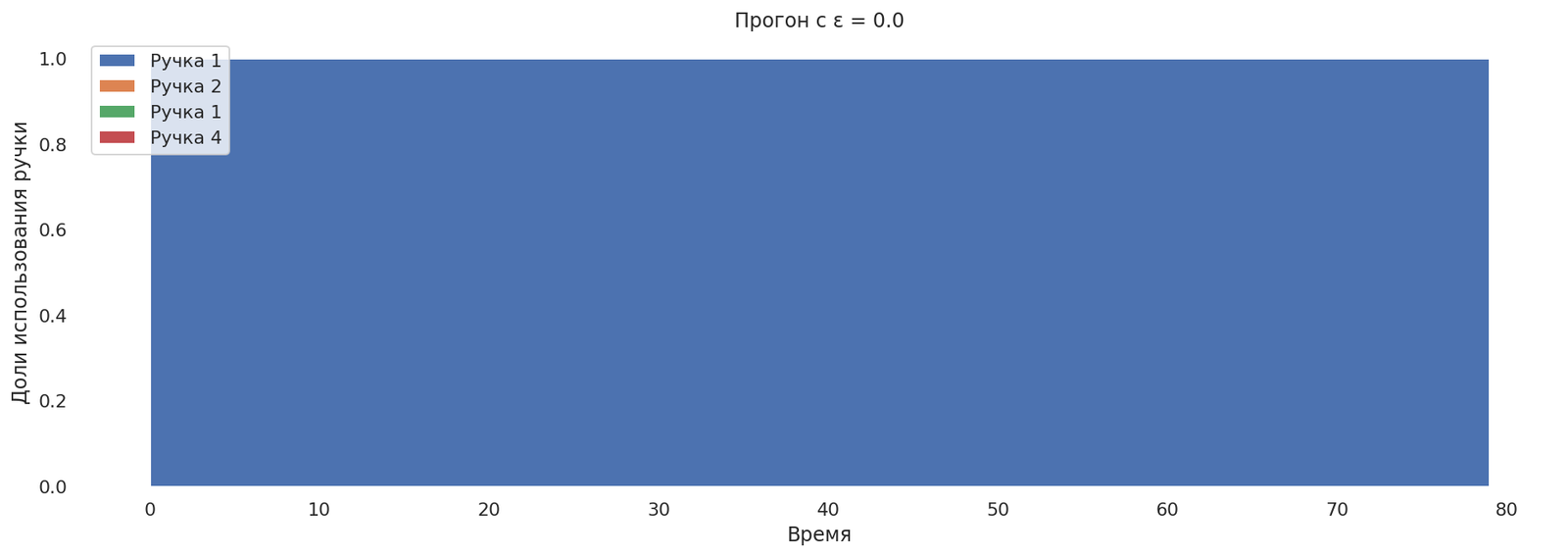
Как и ожидалось, выбралась самая первая ручка, дальше исследования не производятся.

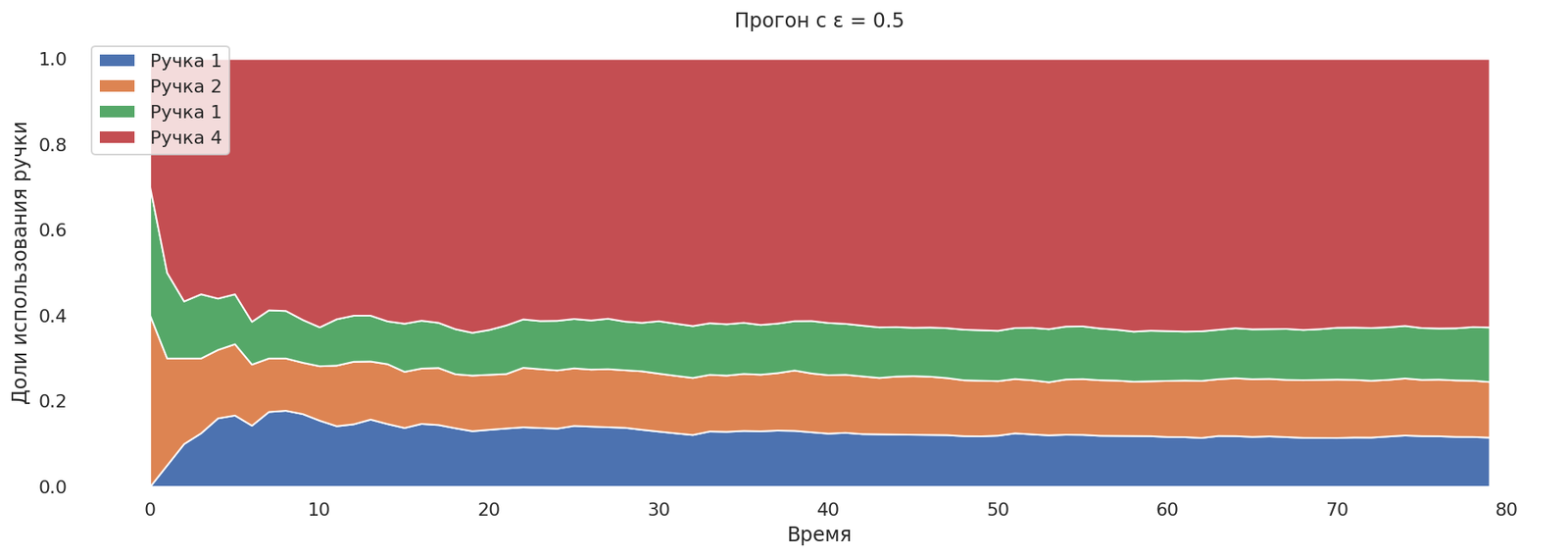
Попробуем выставить ε = 0.5. Самая лучшая ручка найдена, но исследования занимают 50% запусков.

runs = mab_egreedrun(0.5);
plot_runs("Прогон с ε = 0.5",*runs)

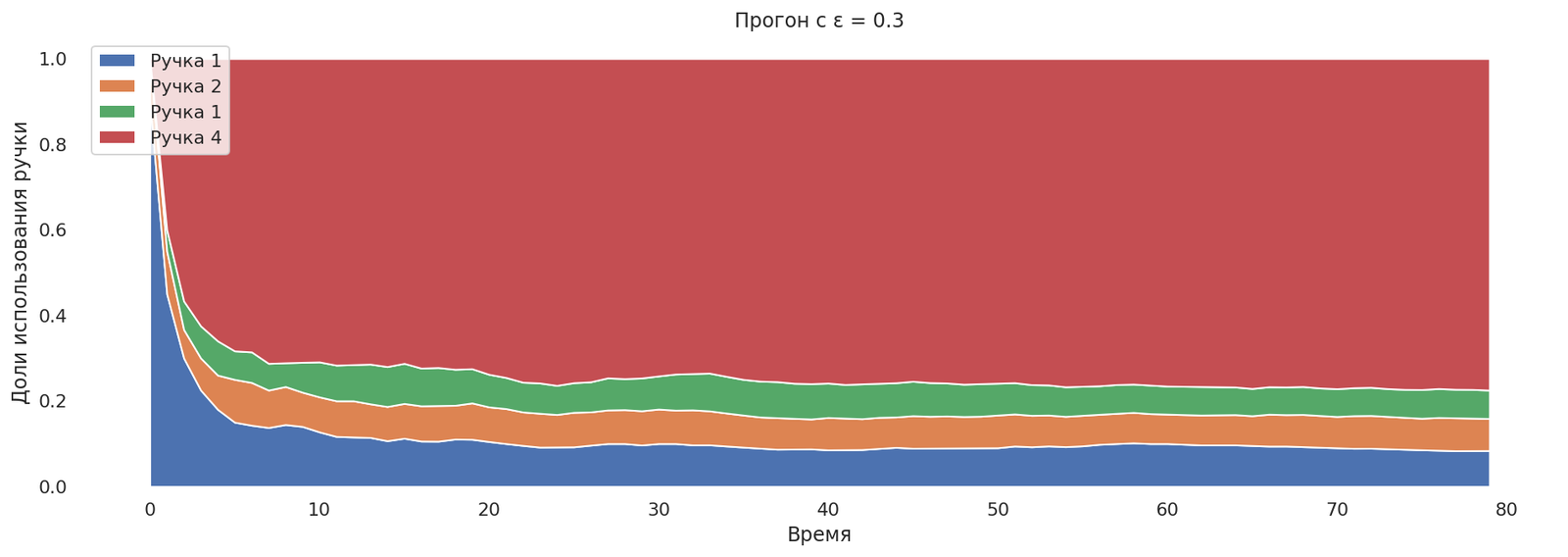
runs = mab_egreedrun(0.3);
plot_runs("Прогон с ε = 0.3",*runs)

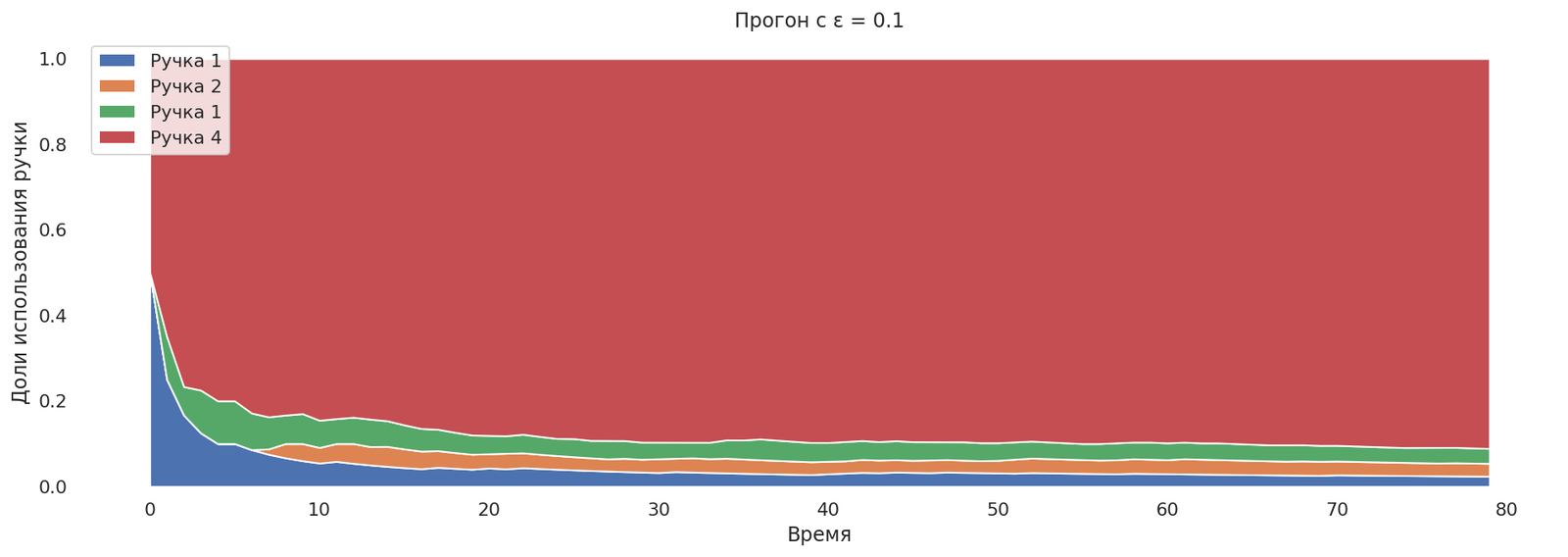
runs = mab_egreedrun(0.1);
plot_runs("Прогон с ε = 0.1",*runs)

Попробуем выставить ε = 0.05.

runs = mab_egreedrun(0.05)
plot_runs("Прогон с ε = 0.05",*runs)

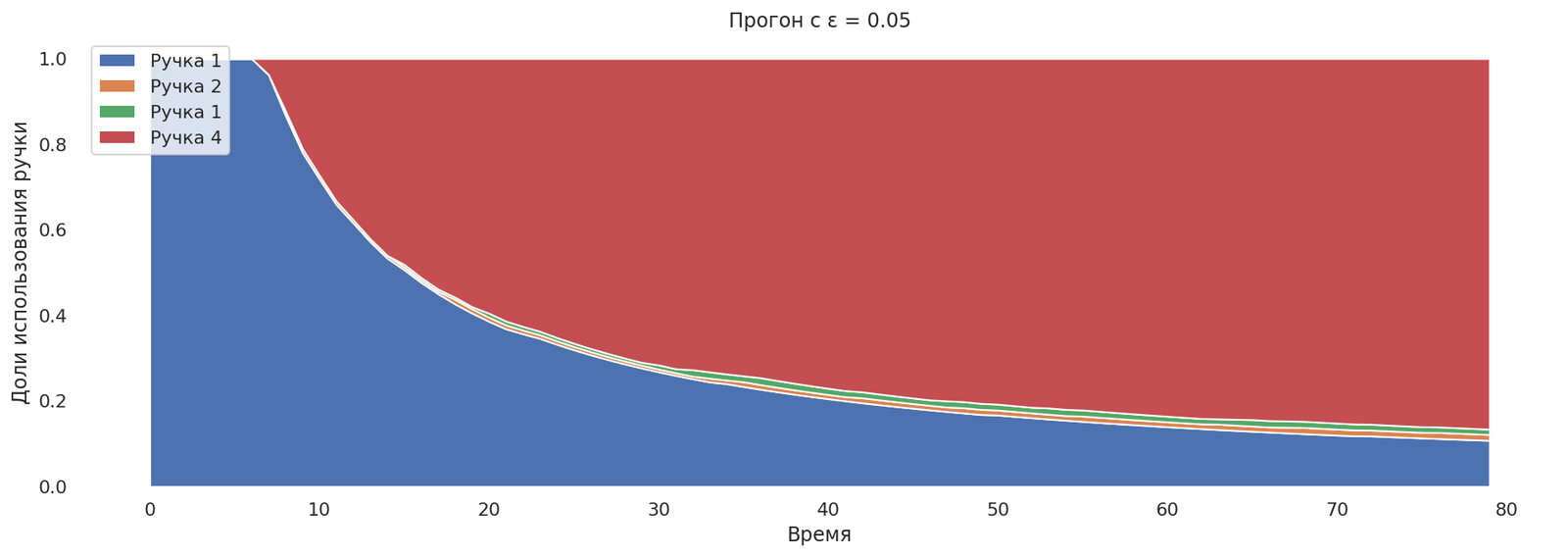
Теперь бандит сходится к лучшей ручке медленно, но при этом в конце концов доля исследований фиксированная. Хорошо или это плохо, зависит от задачи: если ручки меняют своё поведение со временем, то данное свойство желаемо.

Выводы по ε-greedy

Несмотря на простоту и вроде бы адекватность алгоритма, у него есть проблемы:

Мы храним значения всех наград, что затратно.
Если поведение ручек меняется со временем, алгоритм не сможет адекватно среагировать — среднее довольно нечувствительно.
После большого числа использования ручек, когда поведение каждой ручки уже понятно, алгоритм продолжает исследование и получает заведомо плохие награды, чего мог бы не делать.

Что можно сделать:

С первым: заменить среднее, например, на скользящее среднее.
Со вторым: заменить среднее на более чувствительную вещь, например, на медиану. Скользящее среднее также поможет с первой проблемой.
C третьим: уменьшать вероятность ε на исследование со временем. А при релизе новой фичи — повышать.

Это уже будут другие варианты алгоритмов.

Идея в том, чтобы уменьшать долю исследований, отразилась в Aлгоритме UCB1.

Оптимизм перед неизвестностью — Алгоритм UCB1

Вообще можно не кидать монетку для того, чтобы выбрать, что же мы хотим делать, а оценить, насколько больше может быть выигрыш. Мы уже несколько раз дёргали ручку и уже имеем оценку T среднего выигрыша с конкретной ручки. Если ручки со временем не меняют своего поведения, то с каждым использованием ручки надежды недооценить должно становиться всё меньше и меньше.

Формула оценки выводится из неравенства Хёфдинга:

где, g ≥ 0.

В контексте задачи неравенство ограничивает разницу между посчитанным по первым N использованиям конкретной ручки многорукого бандита оценки среднего выигрыша (T) и реального значения среднего E[T] после бесконечного числа попыток.

Вероятность:

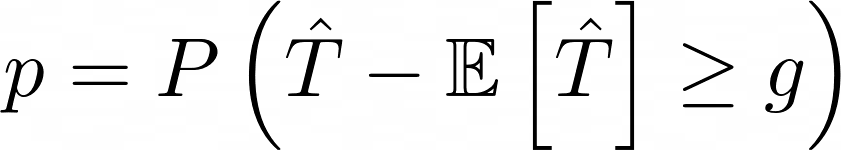
можно трактовать как вероятность превысить выбранный порог g.

Как выбрать такой порог и как задать вероятность p?

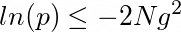
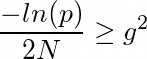
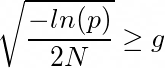
Авторы статьи [2] придумали эвристику:

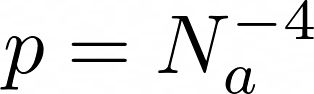
Подставим в выражение р и получим формулу из статьи:

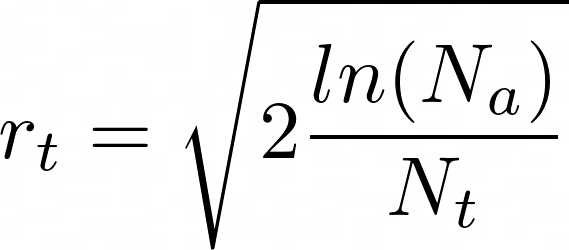
Так мы можем оценить надежду по улучшению t-й ручки бандита.

Если мы хотим получить большую скорость сходимости и больше исследований на первых шагах работы алгоритма, то мы можем использовать другую эвристику, взяв не -4, а большее число. Но можно поступить проще, введя константу с, — результат тот же с точностью до внесения под корень.

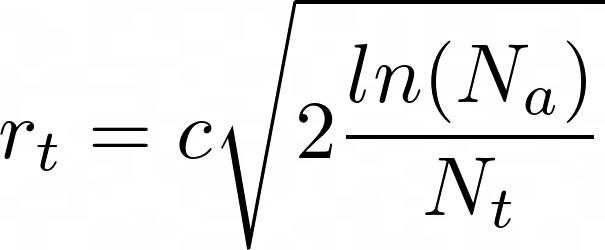
где c > 0 — константа оптимистичности: чем больше она, тем больше мы оптимистичны, Na — сколько раз обращались к бандиту за решением, Nt — сколько раз обращались к конкретной t-ой ручке бандита.

Если же Nt = 0, т.е. ручку бандита ещё никогда не дёргали, то ручка просто считается приоритетнее всех, уже однажды опробованных.

Теперь можно выбрать ручку, рассчитав формулы для каждой из них, и выбрать ту, что даёт максимум:

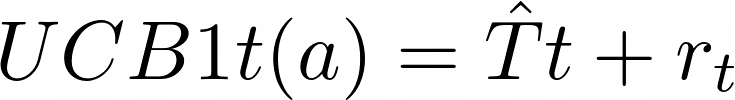
def ucb1_get_best_arm(stats,total_runs):
    top = 0;
    top_arm = 0
    for arm,arm_rewards in stats.items():
        avg_reward =  (1.0/len(arm_rewards)) * sum(arm_rewards)
        c = 1
        arm_runs = len(arm_rewards)-1
        if (arm_runs == 0):
            return arm
        optimism = c*np.sqrt(2*np.log(total_runs)/arm_runs)
        if top < avg_reward + optimism:
            top_arm = arm
            top = avg_reward
    return top_arm

def mab_ucb1(armstats, runs,total_runs):
    arm = ucb1_get_best_arm(armstats,total_runs)
    reward = do_nth_arm(arm)
    
    armstats[arm].append(reward)
    runs[arm] =  runs.get(arm, 0) + 1
    
    return armstats,runs    


def mab_ucb1_run():
    armstats = {x: [y] for x, y in zip(range(4), [0]*4)}  
    runs = {}
    cnt = 0;
    mA = [];mB = [];mC = [];mD = []
    r = [mA,mB,mC,mD]
    for g in range(80):
        n = 10
        for _ in range(0,n):
            _, runs = mab_ucb1(armstats,runs,cnt)
            cnt += 1
    
        [r[x].append(runs.get(x,0)) for x in range(4)]
    return r,armstats

runs,armstats = mab_ucb1_run()
plot_runs("Алгоритм UCB1",*runs)

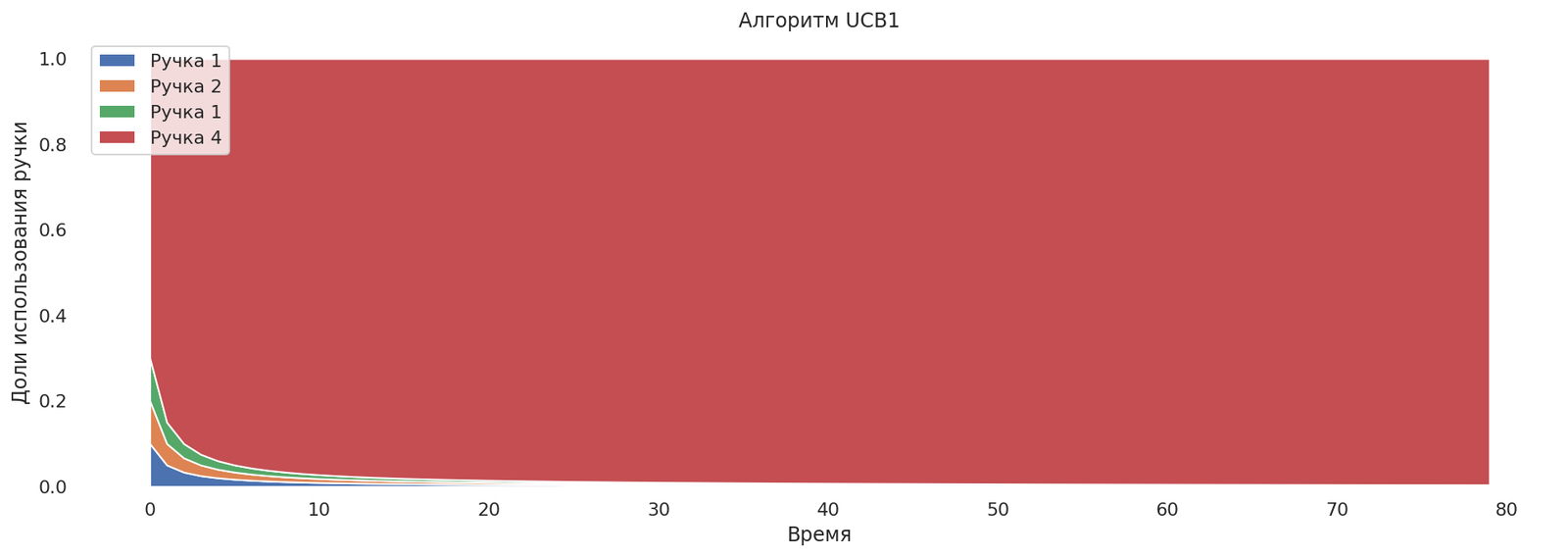
Но на графике не видна проблема, которая может возникнуть на практике. Если ручка обладает большой дисперсией, то многорукий бандит может сначала сойтись к ручке, имеющей меньшее матожидание и меньшую дисперсию, и лишь потом, через продолжительное время, сойтись к нужной, так как исследование будет производиться заметно медленнее.

Попробуем воспроизвести такую ситуацию:

# Зафиксируем seed 
rs = np.random.RandomState(2322)
def arm_A():
    return rs.normal(10, 6)
def arm_B():
    return rs.normal(80, 2)
def arm_C():
    return rs.normal(40, 6)
def arm_D():
    return rs.normal(86, 40)

df = pd.DataFrame({
    "Ручка 1" : [arm_A() for x in range(200)],
    "Ручка 2" : [arm_B() for x in range(200)],
    "Ручка 3" : [arm_C() for x in range(200)],
    "Ручка 4" : [arm_D() for x in range(200)]})

df.plot.hist(bins=40, alpha=0.7).set_title("Кейс ручки с большой дисперсией");

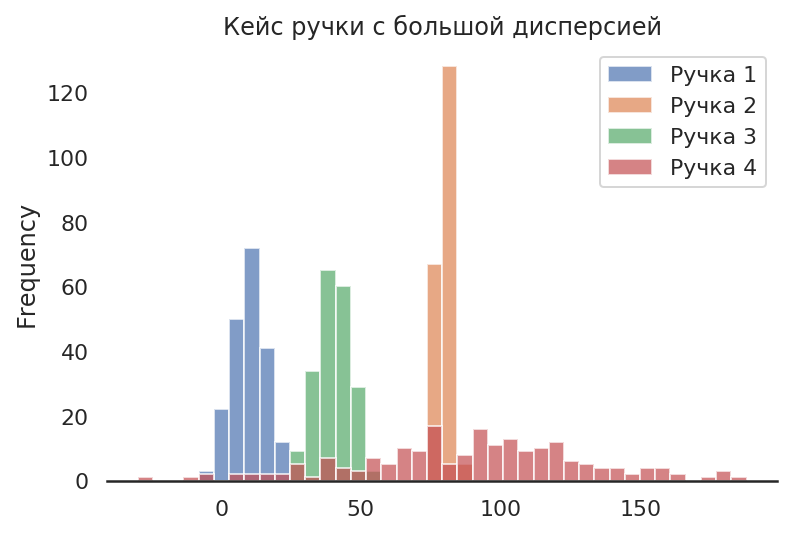
Теперь у нас лучшая ручка обладает большей дисперсией выигрыша, и есть ручка с меньшим средним выигрышем, но и с меньшей дисперсией. Теперь алгоритм может вести себя некорректно.

runs,armstats = mab_ucb1_run()
plot_runs("Алгоритм UCB1 - Сходится уже не всегда",*runs)

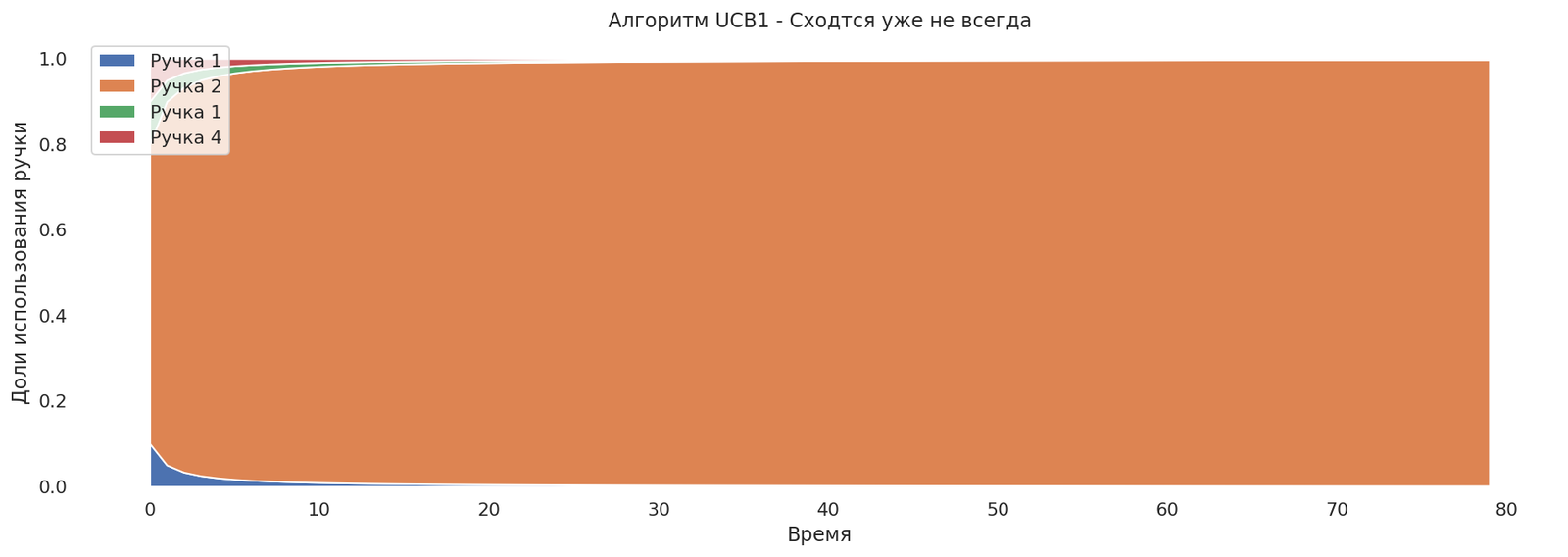
Что можно с этим сделать?

Больше исследовать, настроить константу c — нам нужно больше оптимизма.

Выводы по UCB1

Если бандит не настроен, то может сойтись сначала не к самой лучшей руке и лишь потом, очень медленно, к лучшей.
Сочетает быструю скорость сходимости и не пытается исследовать неперспективные ручки.
Не подходит, если ручка меняет свои свойства.

Что дальше?

Можно ли сделать ещё лучше?

Да, если мы в какой-то степени знаем свойства ручек заранее.

Другим словами, у нас должны быть априорные знания, а в случае распределений — априорные распределения. Подход, в котором вероятность рассматривается как степень незнания, называется Байесовским.

Используя формулу Байеса, мы можем учитывать полученные выигрыши, тем самым уточняя знания о руках многорукого бандита. Мы также можем ограничиться конкретным видом распределения, это тоже априорное знание.

Но это повод для другой статьи.

Выводы

В статье я старался показать, что автоматический подход:

не сложен для понимания,
не сложен в реализации,
имеет преимущества перед А/Б-тестами.

Я надеюсь, статья послужит мотиватором в использовании многоруких бандитов в продуктовой практике как замена А/Б-тестам.

Литература

[1] The Multi-Armed Bandit Problem and Its Solutions.

[2] P. Auer, N. Cesa-Bianchi, and P. Fischer.Finite-time analysis of the multiarmed bandit problem.Machine learning, 47(2):235–256, 2002

Потерянное в коде